Biabırçı olimpiada qalmaqalı böyüyür Professor Təhsil İnstitutuna faktlarla cavab verdi

Rəşid Əliyev,

Riyaziyyat elmləri doktoru, professor

Mənim 10 aprel 2025-ci il tarixli “Təhsil İnstitutunun biabırçı olimpiadası – 30 sualdan 9-u səhvdir” adlı məqaləmlə bağlı Təhsil İnstitutunun açıqlamasında qeyd olunur ki, “Doqquz sualda səhv olduğu ilə bağlı iddialar əsassızdır. Dörd sualda səhv olub və həmin sualların cavabı bütün iştirakçıların xeyrinə həll olunub”. Facebookda izləyicilərdən biri şərh bölümündə qeyd etmişdi ki, “gələcəkdə 30 sualdan 30-u da səhv olacaq. Üstəlik həmin səhvləri heç aşkar edən də tapılmayacaq”. Deyəsən bu proses başlayıb. Ən azından artıq Təhsil İnstitutu səhv və düz tapşırıqları ayırd edə bilmir.

Aydınlıq məqsədi ilə 23 fevral 2025-ci il tarixdə ARTİ tərəfindən təşkil olunan riyaziyyat fənni üzrə RFO Respublika mərhələsinin yuxarı yaş qrupu üzrə yarımfinal turunda iştirakçılara təqdim olunmuş səhv tapşırıqların izahını qeyd edirəm (mötərizədə tapşırığın olimpiadada təqdim olunma nömrəsi qeyd olunub) və təklif edirəm ki, Təhsil İnstitutu inanılmış, təcrübəli müəllimlərdən ibarət Komissiya yaradıb mənim də iştirakımla neçə tapşırığın səhv olduğunu araşdırsın.

1) (1) İki fərqli müəllifin uyğun olaraq 3 və 5 ədəd kitabı var. 3 kitabı olan müəllifin kitabları yanaşı olacaq şəkildə bütün kitabları kitab rəfinə neçə fərqli üsulla yerləşdirmək olar?

A) 120 B) 240 C) 360 D) 720 E) 480

Doğru cavab 4320-dir. Lakin cavab variantları arasında bu cavab yoxdur.

2) (4) ABC üçbucağında B nöqtəsindən AC tərəfinə endirilmiş hündürlüyün oturacağı H nöqtəsidir və O nöqtəsi bu üçbucağın xaricinə çəkilmiş çevrənin mərkəzidir. Fərz edək ki, HO xətti BC parçasının orta nöqtəsindən keçir və , olarsa, AB parçasının uzunluğu nə qədərdir?

A) 20 B) C) 25 D) 30 E) 35

Üçbucağın itibucaqlı və korbucaqlı olmasından asılı olaraq iki fərqli cavab var (bax: şəkil 1 və şəkil 2):

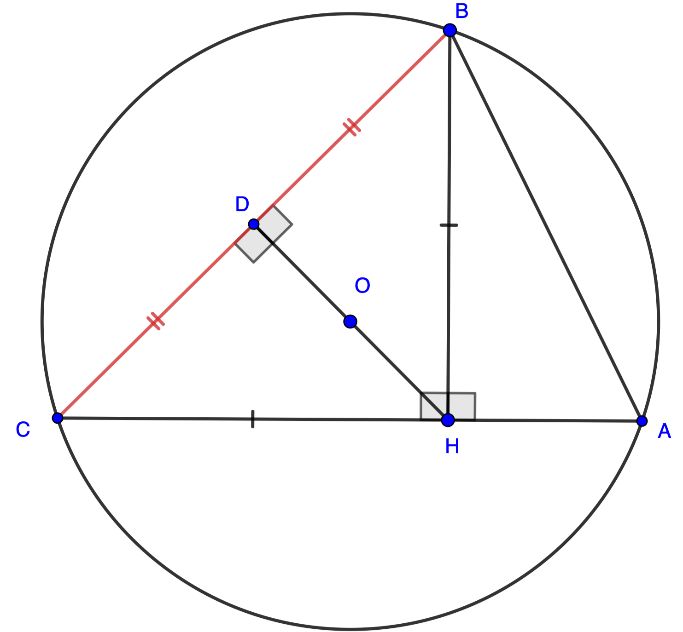
Şəkil 1

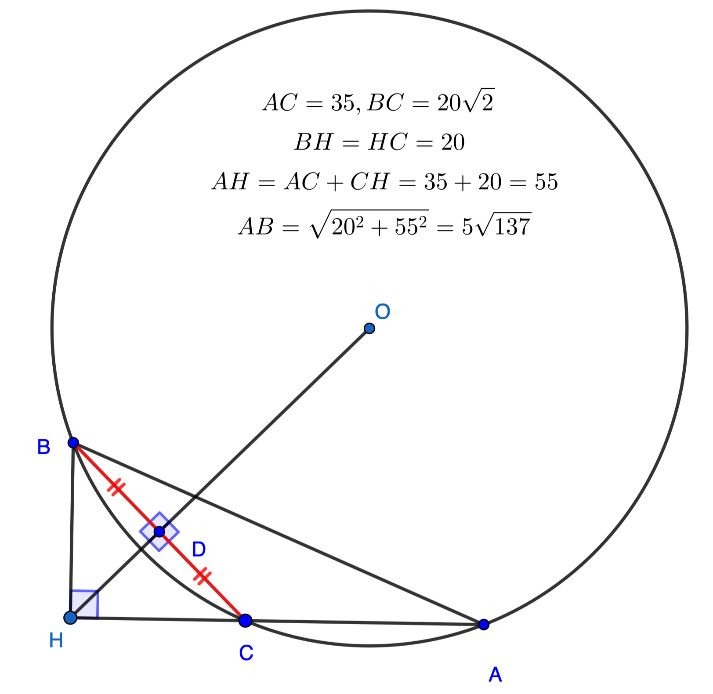
Şəkil 2

3) (11) ABC üçbucağının daxilinə çəkilmiş çevrənin mərkəzi İ nöqtəsidir. İ və B nöqtələrindən keçən çevrə AB və BC-ni uyğun olaraq M və N nöqtələrində kəsir. AC=10 olarsa AM+CN məsafəsini tapın.

A) 10 B) C) 14 D) 16 E) 20

Cavab birqiymətli deyil. BC üzərində C nöqtəsindən kifayət qədər uzaq olan ixtiyari N nöqtəsi götürüb, N, İ və B nöqtələrindən keçən çevrə çəksək (bir düz xətt üzərində olmayan ixtiyari 3 nöqtədən keçən çevrə var) və bu çevrənin AB ilə ikinci kəsişmə nöqtəsini (birincisi B nöqtəsidir və bu çevrə AB-yə toxunmur) M ilə işarə etsək olar (bax: şəkil 3):

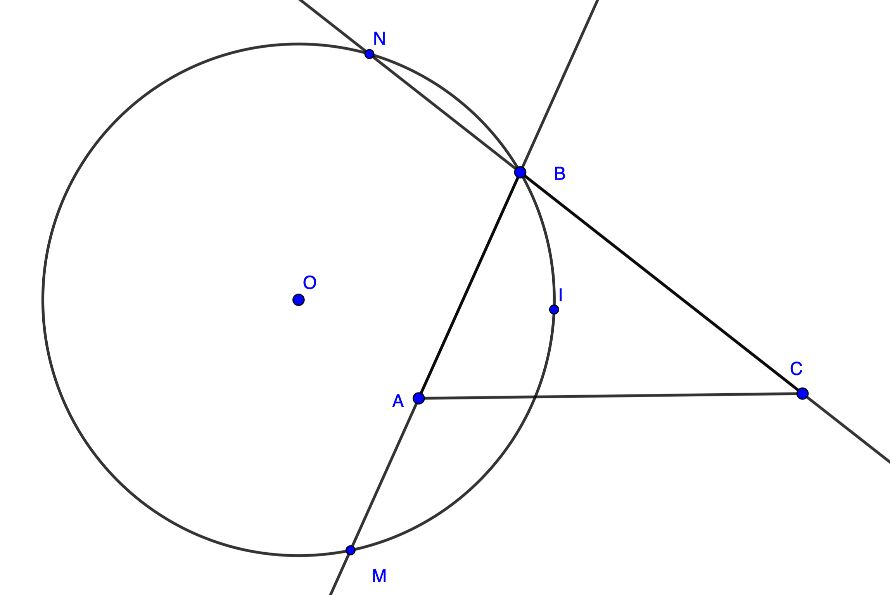
Şəkil 3

4) (13) tənliyinin həlli müsbət tam ədədləri üçün formasında olarsa, cəmini tapın.

A) 7 B) 8 C) 9 D) 10 E) 11

Cavab birqiymətli deyil. Tənliyin həlli olan ədədini üç müxtəlif üsulla şəklində yazmaq olar: . Belədə cəmi üçün də 3 müxtəlif cavab alırıq və bu cavablardan 2-si cavab variantları arasındadırlar.

5) (14) tənliyini ödəyən tam həllərinin cəmi neçədir?

A) 4 B) -8 C) 9 D) -9 E) 12

Sual düz deyil. Verilən tənliyi yalnız dəyişəninə nəzərən həll ediriksə parametrinin necə olduğunu bilmədən həllər cəmini tapa bilmərik. Belə ki, parametri sərbəstdirsə, onda verilən tənliyin dəyişəninə nəzərən sonsuz sayda tam həlli var.

6) (17) Rəqəmləri hər hansı üçbucağın tərəfləri olan bütün üçrəqəmli ədədlərin sayını tapın.

A) 316 B) 363 C) 380 D) 410 E) 455

Doğru cavab 369-dur. Lakin cavab variantları arasında bu cavab yoxdur.

7) (28) İki dost kafeyə getməyə və burada 18:00 ilə 20:00 arasında görüşməyə razılaşırlar. Əgər hər hansı biri kafeyə 19:30-dan gec gəlməyibsə, onda o, 30 dəqiqə gözləməlidir. Əgər hər hansı biri kafeyə 19:30-dan gec gəlibsə, o, 20:00-a qədər gözləməlidir. Əgər p ədədi bu iki dostun kafedə görüşmə ehtimalı olarsa, 16p ifadəsinin qiyməti nə qədərdir?

A) 7 B) 8 C) 9 D) 10 E) 11

Tapşırığın şərtlərində əskikliklər var. Bu şərtlər daxilində dostların görüşmə ehtimalını tapmaq olmaz. Çünki, dostların kafeyə gəlmə ehtimallarının necə paylandığı və dostların kafeyə mütləq 18.00 ilə 20.00 arasında gələcəkləri bilinmir. Bundan əlavə məsələ həndəsi ehtimal vasitəsilə həll olunur ki, bu mövzu da 2024-2025-ci tədris ili üçün Riyaziyyat fənni üzrə Respublika Fənn Olimpiadalarının proqramına daxil edilməyib.

(bax: https://arti.edu.az/wp-content/uploads/2024/11/RFO-Riyaziyyat-proqram.pdf )

8) (5) ifadəsinin qiyməti aşağıdakılardan hansına bərabərdir?

A) 0 B) 1 C) 2 D) 3 E) 4

Loqarifm mövzusu 2024-2025-ci tədris ili üçün Riyaziyyat fənni üzrə Respublika Fənn Olimpiadalarının proqramına daxil edilməyib.

9) (2) tənliyinin həlləri cəmi neçədir?

A) 13 B) 15 C) 17 D) 19 E) 20

Tənliyin həllər cəmini tapmaq üçün əvvəlcə tənliyi loqarifmləmək lazımdır. Loqarifm mövzusu isə 2024-2025-ci tədris ili üçün Riyaziyyat fənni üzrə Respublika Fənn Olimpiadalarının proqramına daxil edilməyib. Təhsil İnstitutunun özünün tərtib etdiyi proqramdan xəbərsiz olması inandırıcı görünmür.